09.11.2011 / Fikri Akdeniz - Müzikte Altın Oran ve Fibonacci Dizisi

     Çok sayıda kişi sezgisel olarak matematik ve müzik arasında bir ilişki olduğunu söyler. Müzik teorisyenleri, müziği anlamak için çoğu kez matematik kullanırlar (David Wright, Mathematics and Music, 2009, Ams). Matematiğin tanınmış oranı olan ve doğada bir güzellik ölçütü olarak belirtilen  = 1, 618... sayısı ile ifade edilen “Altın Oran” müzikte de yaygın etkiye sahiptir. Örneğin, müzik aletlerinin yapımını etkilemiştir. Müzik aletleri çoğu kez  sayısı temel alarak yapılır. Keman tasarımında olduğu gibi yüksek kalitede ses telinin tasarımında da “Fibonacci Sayıları” ve  kullanılmıştır. Aşağıda orkestra müzik aletlerinin en güzellerinden biri olan keman üzerindeki altın oranlar görülmektedir.

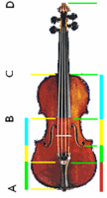
     AB / BC =  ve AC / CD =  olmasının dışında AD / AC = AC / AB = CD / BC =  dır.

     1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,,, sayılarının oluşturduğu diziye “Fibonacci Dizisi” denir. “Fibonacci Dizisi” yaşam, güzellik ve sanatsal kavramların oluşturulmasında ortaya çıkmaktadır. Ardışık iki sayının toplamı üçüncü sayıyı vermektedir. “Fibonacci Dizisi”ndeki ardışık iki sayının oranını alırsak, aşağıdaki kesirleri ve karşılık gelen ondalıklı sayıları buluruz.

     Oranlara karşılık gelen sayıların değerleri arttıkça oran değerlerinin hangi sayıya yaklaştığını görmek çok kolaydır. Oranların özel bir sayıya doğru gittiği görülür ki bu değere “Altın Oran” denir. Yaklaşık olarak bu sayının değeri  = 1,618034 dir. Müzik de aşağıda görüldüğü gibi “Fibonacci Dizisi”ne dayanmaktadır.

     Her notanın kendi oktavının aralığında 13 nota vardır. Bir skala 8 notadan oluşur, bunlarda 5. ve 3. notalar bir arada çalınan tüm notaların temelini oluşturur  ve bunlar, temel nota olan  skalanın 1. notasından 2 aralık uzaktadır.

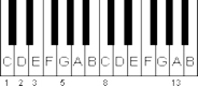
     Piyanonun tuşları da (C den C ye) “Fibonacci Sayıları”na uymaktadır. Skala içinde sekizi beyaz, beşi siyah olan 13 tuş bulunmaktadır. Bunlar da 3 ve 2’li guruplara ayrılmıştır. Görüldüğü gibi skala üzerinde 1., 2., 3., 5., 8. ve 13. notalar ilk altı “Fibonacci Sayısı” olan 1, 2, 3, 5, 8 ,13’dür.

     Altın oran bir doğru parçasını ya da bir müzik bestesini iki parçaya bölen bir matematiksel formüldür. Fiziksel bir kanıt olmasa da Mozart’ın yaptığı müzikte Fibonacci dizisini kullandığını görmek zor değildir. Mozart yazdığı piyano sonatını altın oranı yansıtacak biçimde dikkat çeken bir sayı ile iki parçaya ayırmıştır. 19’cu yüzyıl Çek bestecilerinden Antonin Dvorak “Mozart bir güneştir” demiştir. Pek çok kişi Mozart’ın müziğinin ışıl ışıl parladığı konusunda fikir birliğindedir.  Muhtemelen O’nun müzik dehası günlük olaylardan ilham alıyordu. Öte yandan, matematiksel denklemlerle müzikteki beste ölçümlerine sahipti. Matematikçi John F. Putz, Mozart’ın müziğindeki yapıya dikkat çekmiştir. Putz 1995’de “Mathematics Magazine” 68 (4), 275-282 dergisinde yayınlanan araştırma makalesinde Mozart’ın piyano sonatlarında altın oran bölünmesi olup olmadığına yanıt aramıştır. Mozart’ın döneminde piyano sonatları geleneksel olarak iki parçaya ayrılırdı. (1) Anlatım (Müzik temasının işlendiği daha kısa olan parça); ve (2) Geliştirme ve tekrarlama (recapitulation). Mozart’ın C Major Sonat No. 1’i 100 ölçüden oluşuyor ve 38 ve 62 ölçülük iki parçaya ayrılmıştır. 38/62=0,613 değeri yaklaşık olarak  – 1 = 0,618 değerine oldukça yakındır. Putz, Mozart’ın piyano sonatlarındaki bölümlerde yaptığı analiz sonucunda  altın oran olduğu sonucuna varmıştır.

     Yirminci yüzyılın en önemli müzisyenlerinden Macar besteci Bela Bartok (1881-1945) ve Fransız mimar Le Corbusier (1887-1965) çalışmalarında bilinçli olarak altın oranı yerleştirmişlerdir. Dünyaca ünlü Alman klasik müzik bestecisi Bach (1685-1750)’ın da eserlerinde altın oran kullandığı iddiaları bulunmaktadır. Fransız besteci ve piyanist Erik Satie (1866-1925) “Sonneries de la Rose Croix” da dahil olmak üzere parçalarının çoğunda altın oranı kullanmıştır.

     “Illinois Üniversitesi” müzik Profesörü Sever Tipei’nin (1943-) bir öğrencinin müzikte altın oranla ilgili sorduğu soruya verdiği yanıt aşağıdaki gibidir:

     “Altın oran aslında pek çok kompozisyonda bulunabilir, çünkü zamanın bölünmesiyle ilgili bir ‘doğal’ yoldur. Mozart, Beethoven, Chopin, vs. tarafından yapılan pek çok çalışmada bulunabilir. Soru şudur: Sezgisel olarak mı yoksa bilinçli bir şekilde mi kullanıldığıdır.”

     Öte yandan, Fransız besteci Debussy (1862-1918) ve Macar besteci Bartok (1881-1945) gibi müzisyenler bilinçli girişimler yaparak bu oranı ve Fibonacci dizisini kullandılar. Bartok, semitonların Fibonacci sayılarıyla ifade edilebilen büyüklükteki aralıklarda melodiler yazdı. Ayrıca altın orana karşılık gelen oranlardaki parçalarla formal kesitleri böldü. Çok ayrıntısına girmeden, Debussy de bazı müziklerinde bunu yaptı. Çağdaş müzisyenler ve besteciler de altın oran ve Fibonacci sayılarından yararlanmaktadırlar.

     09.11.2011, Adana